Подскажите, пожалуйста!
Шанс закинуть себе блесХП через SOES равен 20%.
Так понимаю в таком случае используется непрерывный диапозон чисел с границей в 20%.
1. Хотел бы понять с какой стороны идет граница удачного прохождения с нижней или верхней?
2. И аналогично понять с какой стороны идет порог по шансу физического крита? 3. Магического крита?
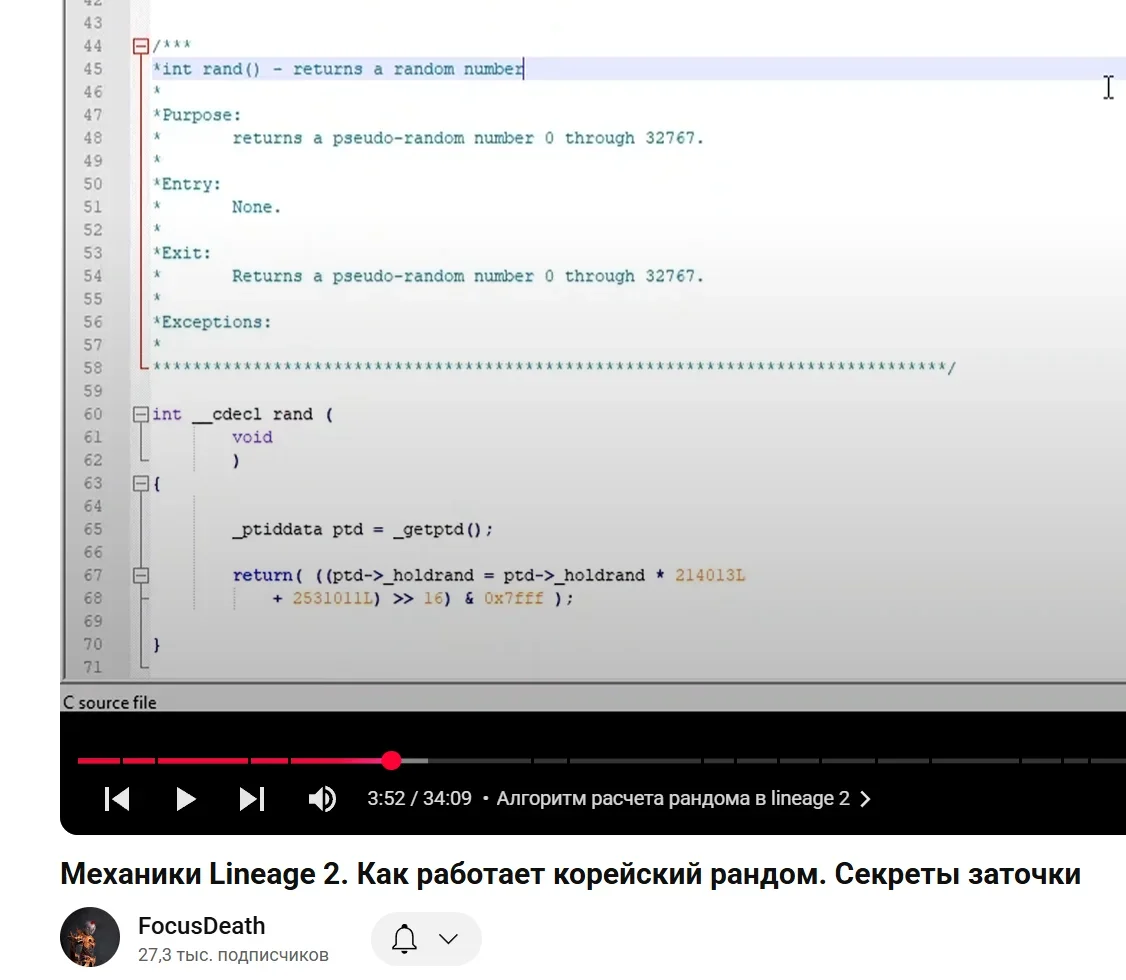
Что имею ввиду. По ответу Мастера Томы вижу, что удачная заточка считается от нижнего порога. Получается если шанс 40%, то из 32 768 удачные числа будут до 13 107.
Если точить шмотки с 5 на 6, там шанс 25%, то получается удачные числа будут до 8 192. Хочу попробовать нащупать волну/такт через SOES, если у него тоже используется нижний порог.
Шанс закинуть себе блесХП через SOES равен 20%.
Так понимаю в таком случае используется непрерывный диапозон чисел с границей в 20%.
1. Хотел бы понять с какой стороны идет граница удачного прохождения с нижней или верхней?
2. И аналогично понять с какой стороны идет порог по шансу физического крита? 3. Магического крита?
Что имею ввиду. По ответу Мастера Томы вижу, что удачная заточка считается от нижнего порога. Получается если шанс 40%, то из 32 768 удачные числа будут до 13 107.
Если точить шмотки с 5 на 6, там шанс 25%, то получается удачные числа будут до 8 192. Хочу попробовать нащупать волну/такт через SOES, если у него тоже используется нижний порог.
ладно раз уж тут декомпилами кидаем... вот чуток более читабельный
C++:
char __thiscall CWorldItem::EnchantItem(CWorldItem *this, CWorldItem *itemToEnchant, CWorldUser *user)
{
int enchantLevel; // esi@3
CSharedItemConstData *constSharedData; // eax@4
CUserSocket *userSocket; // eax@11 MAPDST
double dice2; // st7@28
int itemClassId; // [sp-4h] [bp-3Ch]@11 MAPDST
int v11; // [sp+0h] [bp-38h]@1
double dice; // [sp+Ch] [bp-2Ch]@9
double chance; // [sp+14h] [bp-24h]@6
int *v15; // [sp+28h] [bp-10h]@1
int v16; // [sp+34h] [bp-4h]@1
v15 = &v11;
v16 = 0;
if (...